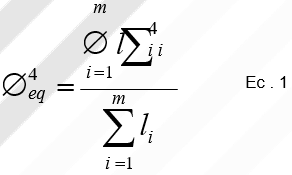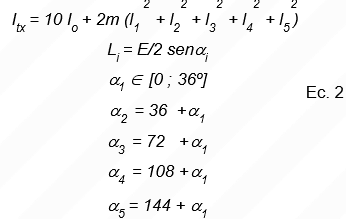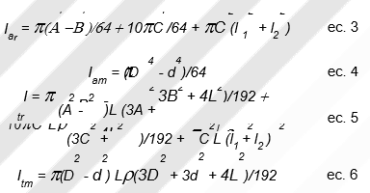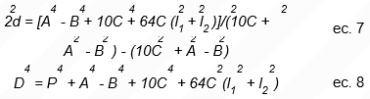Modelaje Elastomásico del Rotor de una Turbina a Gas
El primer paso para hacer una auditoría rotodinámica a una turbomáquina, consiste en modelar el rotor. Sin embargo, no está establecida una metodología estándar para este propósito, situación que dificulta el modelar rotores de geometría compleja.
Este trabajo presenta la construcción y validación de un modelo elastomásico del rotor de una turbina a gas que está sometida a una auditoría rotodinámica.
La generación del modelo requirió hacer registros dimensionales e inerciales (usando planos del fabricante en unos casos y mediciones en otros) de componentes individuales y subensamblajes. Por su parte, la validación fue hecha progresivamente, haciendo coincidir primero los parámetros estáticos (peso y centro de gravedad) del modelo con los medidos en campo, para luego hacer coincidir los autovalores y autovectores simulados con el programa CRTSP2 de velocidades críticas de la Universidad de Virginia (ROMAC), con aquellos medidos en una prueba de impacto.
DESCRIPCIÓN DE LA MÁQUINA
La turbina objeto de este trabajo es del tipo industrial accionada a gas, y con 44 años en operación. El rotor pesa 5400 kg y mide 4 m entre cojinetes. Entrega 9600 hp ISO a 6200 rpm. Su servicio es accionamiento de un compresor centrífugo de gas.
Lagoven, S.A., filial de petróleos de Venezuela (PDVSA), posee un total de 42 de estas turbinas distribuidas en tres (3) plantas compresoras de gas natural costa afuera, apoyando la extracción de crudo por levantamiento artificial y la producción de GLP a través de un ciclo de refrigeración.
DESCRIPCIÓN DEL PROBLEMA ROTODINÁMICO
El balanceo en sitio de estas turbinas, como parte del mantenimiento mayor, toma aproximadamente dos (2) días en ser ejecutado. Sin embargo, algunos rotores presentan un comportamiento atípico en su respuesta al desbalance, requiriendo así hasta cuatro (4) días de labor para ser balanceados.
Tomando en cuenta que cerca de diez (10) turbinas son balanceadas cada año, se plantea entonces la necesidad de desarrollar un método analítico de balanceo en sitio, que permita balancear en forma confiable y rápida (1 día) estas turbinas, haciendo uso del estado del arte en herramientas computacionales en el área de dinámica de rotores. Esto representaría un ahorro mínimo de dos (2) semanas de labor al año, con el correspondiente incremento de producción. La dificultad para balancear esta influenciada por el hecho que la máquina opera cerca de la tercera velocidad crítica. Están disponibles en sitio sólo tres (3) de los cuatro (4) planos de balanceo existentes en el rotor.
DESCRIPCIÓN DEL ROTOR
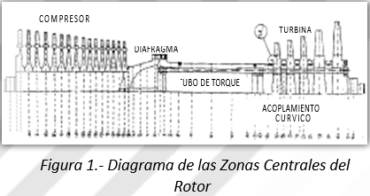
La Figura 1 es un diagrama del rotor donde sólo se muestran las zonas de interés (se excluyen los extremos). Las dieciséis (16) etapas de compresión son anillos fijados con ajuste prensado a un eje sólido que termina en un diafragma de forma acampanada. Por su parte, las cinco (5) etapas de potencia son discos unidos entre si a través de acoples cúrvicos que permiten la dilatación térmica.
Una sección tubular, llamada tubo de torque, conecta las etapas de potencia con el diafragma a través de una brida. La sección constituida por el tubo de torque y las etapas de potencia se mantiene unida por efecto de diez (10) pernos largos. Los extremos (no mostrados) van fijados también con tornillos al rotor.
Adicionalmente se muestran los planos de balanceo espaciados uniformemente a lo largo. La Figura 1 presenta las estaciones de masa del modelo (70 en total), que fueron seleccionadas de acuerdo a los elementos mecánicos de interés presentes en el rotor.
Uno de los objetivos ulteriores de este trabajo es determinar cómo influyen en la dinámica de este rotor la gran cantidad de uniones apernadas.
REPRESENTACIÓN ELASTOMÁSICA
La Figura 2 es una representación del modelo del rotor del tipo masas concentradas y eje sin masa. El proceso de modelaje redujo todo a una colección de anillos y discos equivalentes, unidos axialmente.
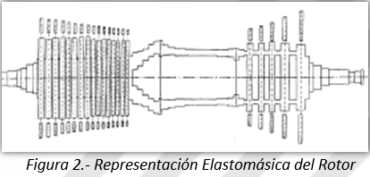
Los álabes, de distribución discreta, conservan su geometría original, pero convertidos en anillos continuos de densidad reducida. Las ruedas del compresor fueron convertidas en anillos lisos, montados sobre el eje sólido. El diafragma quedó conformado por una colección de anillos de diferentes diámetros.
Etapas de Compresión
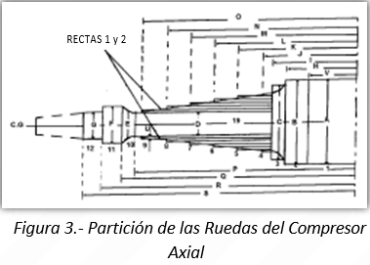
La geometría y las propiedades inerciales y elásticas de las ruedas del compresor eran desconocidas. El tratamiento consistió en dividir una rueda genérica en las 19 particiones mostradas en la Figura 3, para luego parametrizar los cálculos volumétricos e inerciales de las 16 etapas diferentes. En la Figura 2 se observan los anillos lisos equivalentes, con diámetros ligeramente reducidos por efecto de las curvaturas de las ruedas originales.
El ajuste prensado de las ruedas sobre el eje, fue modelado usando el diámetro exterior de las ruedas como diámetro para la rigidez del rotor.
Diafragma
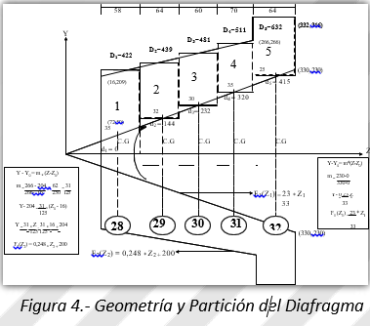
El diafragma es una pieza formada por dos conos de diferentes pendientes, tal como se aprecia en la Figura 4. Se desarrollaron las ecuaciones cartesianas de los dos conos, (curvas F1 y F2) para calcular el volumen del diafragma por métodos integrales.
Se hizo coincidir el volumen de las cinco (5) particiones mostradas en la Figura 4, con el volumen calculado previamente. Dichas particiones fueron hechas de manera arbitraria, con la intensión ulterior de ubicar las estaciones 28 a 32 en sus centros. Finalmente se calcularon los diámetros axialmente equivalentes entre las estaciones 28 a 32.
Diámetros Axialmente Equivalentes. Un Hallazgo
Durante el desarrollo de este trabajo se desarrolló una fórmula simple y útil para el cálculo de un diámetro equivalente para una sección de eje con varios cambios de diámetros, a saber:
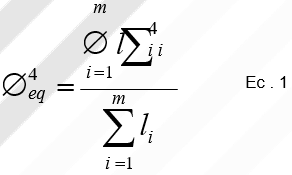
donde фeq = diámetro axialmente equivalente de la sección
фi = diámetro de la subsección i
li = longitud de la subsección i
m = nro. de diferentes diámetros en la sección
Este procedimiento se ajusta dentro del 2% al procedimiento del área bajo la curva del momento flector, con la gran ventaja que es extremadamente rápido.
Ensamblaje Apernado. Tubo de Torque y Acoples Cúrvicos
El ensamblaje apernado comprende lo correspondiente al tubo de torque y las etapas de potencia (ver Figura 1) y está caracterizado por poseer diez (10) pernos largos que lo mantienen axialmente unido.
Invariabilidad del Momento Transversal de Inercia con Respecto al Giro del Rotor
Se consideró conveniente verificar el comportamiento inercial y elástico del ensamblaje tube de torque-pernos y del ensamblaje acoples cúrvicos-pernos antes de reducir estos ensamblajes a anillos equivalentes.
en las figuras 5 y 6 se presenta al ensamblaje apernado en dos posiciones diferentes durante el giro. El momento transversal de inercia de los diez (10) pernos con respecto a un eje horizontal, esta dado por la Ecuación 2 para un ángulo *1 variando entre 0 y 36 º:
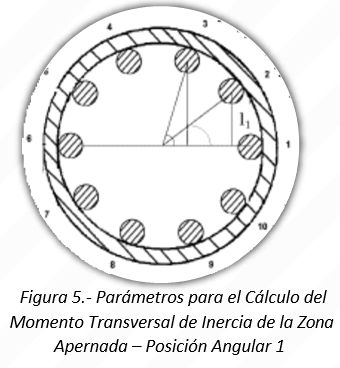
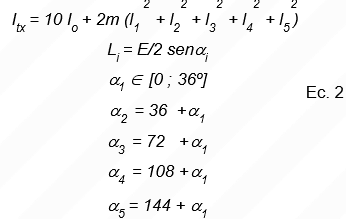
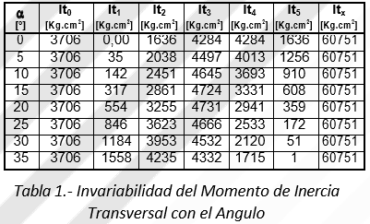
Para evitar desarrollos trigonométricos tediosos, se desarrolló la Tabla 1 mostrando el resultado de calcular Itx para varios valores de α1
Obsérvese que el momento transversal de inercia se mantiene constante a medida que el rotor gira.

Anillos Equivalentes
La estrategia de modelaje en este caso fue convertir cada zona del tubo de torque, sin cambios de diámetros, en un anillo equivalente desde el punto de vista elástico e inercial, ver Figura 7. Esto se logró igualando el momento transversal de inercia y el momento de área de segundo orden de la configuración real, con los correspondientes del anillo modelo equivalente.
Definimos:
Iar = Momento de área de segundo orden. Configuración real.
Iam = Momento de área de segundo orden. Anillo equivalente.
It = Momento transversal de inercia. Configuración real.
Itm = Momento transversal de inercia. Anillo equivalente.
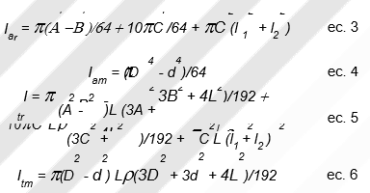
Haciendo:
- 3 = ec. 4, y
- 5 = ec. 6,
obtenemos un conjunto de dos ecuaciones con dos (2) incógnitas, D y d (Figura 7), cuya solución es:
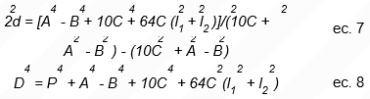
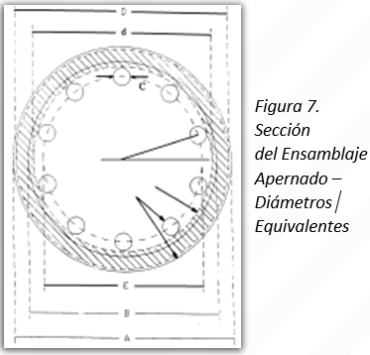
Se observa en las Ecuaciones 7 y 8 que D y d son independientes de la longitud del tramo en cuestión, tal como era esperado. Por lo tanto, se pueden reducir todas las porciones del tubo de torque y acoples cúrvicos a anillos equivalentes con diámetros obtenidos a partir de las Ecuaciones 7 y 8.
Verificación de la Conservación de la Masa Despejando (l12 + l22) de las Ecuaciones 7 y 8, e igualando se obtiene:
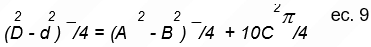
lo cual expresa, en términos de área (S) de la sección transversal que

o lo que es igual decir, para una L (longitud) y una ρ (densidad) arbitrarios,

Etapas de Potencia
De las ruedas de las etapas de potencia eran conocidas solamente las propiedades elásticas (tipo de acero). La geometría fue medida en sitio y las propiedades inerciales fueron calculadas.
El tratamiento consistió en dividir una rueda genérica en las 11 particiones mostradas en la Figura 8, para luego parametrizar los cálculos volumétricos e inerciales de las 5 diferentes etapas. Se tomó en cuenta que, en este caso la rueda constituye en sí el eje elástico, razón por la cual la zona del acople cúrvico fue separada de la rueda. Se definieron tres (3) estaciones de masa en cada rueda para evitar el uso de diámetros equivalente entre secciones disímiles, ver Figura 1.

En la Figura 2 se observan los discos lisos equivalentes, con diámetros ligeramente reducidos por efecto de las curvaturas de las ruedas originales.
Álabes
El siguiente tratamiento fue aplicado por igual a todos los álabes de rotor.
La distribución discreta de los álabes fue modelada como un anillo continuo de densidad reducida, manteniendo la misma proyección tangencial y el mismo radio de giro. Esto puede observarse en la Figura 2, donde el perfil de los álabes aparece separado de sus ruedas por efecto de la disminución en los diámetros mencionada anteriormente.
Solamente la mitad del peso medido en sitio fue asignada a la zona expuesta del álabe.
VALIDACIÓN ESTÁTICA. MASA Y CENTRO DE GRAVEDAD GLOBALES
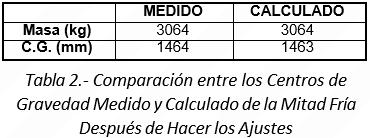
En la primera comparación entre el rotor modelo y el real, se obtuvieron diferencias de 44 kg en peso y 10 mm en la ubicación del centro de gravedad. La calibración se hizo agregando esos 44 kg de masa a la estación 11, primer plano de balanceo, ya que inicialmente se desconocía su volumen (geometría) y masa. De esta manera el centro de gravedad del modelo coincidió casi exactamente con el medido.
En las Tablas 2 y 3 se puede apreciar que el error estático del modelo, después de la calibración, es despreciable.
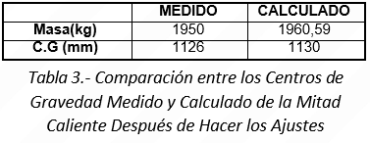
VALIDACIÓN DINÁMICA
Prueba de Impacto
El problema de balanceo implica hacer un análisis dinámico que evalúe la ubicación de los planos de balanceo existentes con respecto a los tres (3) primeros modos de vibración. Por esta razón es importante que el modelo reproduzca con precisión tanto las velocidades críticas, como sus modos de vibración asociados.
La prueba de impacto sobre el rotor se realizó con la intensión de determinar sus frecuencias naturales y modos de vibración libre-libre, y validar los correspondientes del modelo elastomásico construido.
El rotor completo (con álabes instalados) fue suspendido horizontalmente con cuerdas verticales en los muñones. El rotor fue instrumentado colocando siete (7) acelerómetros uniformemente espaciados a todo lo largo, y conectados a un sofisticado analizador de ocho (8) canales simultáneos. El octavo canal del analizador fue conectado a un martillo instrumentado, que fue utilizado para golpear al rotor, excitar sus vibraciones libre-libre, y medirlas.
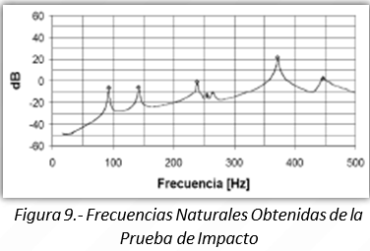
La Figura 9 presenta la función de transferencia obtenida de promediar diez (10) respuestas en este ensayo. Los tres (3) primeros picos corresponden a las tres primeras frecuencias naturales en modo libre-libre, que fueron las utilizadas para calibrar/validar el modelo.
Calibración del Modelo
Las premisas establecidas antes de calibrar el modelo fueron las siguientes:
- La geometría del rotor era
- La metalurgia del rotor era
- El efecto del ensamblaje era
El proceso de calibración se realizó en tres (3) pasos. En el primero, se analizó la sensibilidad de la respuesta del rotor ante los cambios en el módulo de elasticidad (ME) del ensamblaje apernado (tubo de torque + discos de potencia), estaciones 33 a 63, utilizando el ME del acero Inconel X750 (material de los pernos) y el ME del acero Discaloy (material de los discos). Se llegó a la conclusión de que el Discaloy reproduce mejor el comportamiento del rotor.
En un segundo paso se variaron los diámetros de rigidez y los módulos de elasticidad de las estaciones 11 a 27 (etapas de compresión), para incorporar el efecto del ajuste prensado de las ruedas del compresor. También se variaron los módulos de elasticidad de las estaciones 33 a 63 (ensamblaje apernado), para incorporar el efecto de los pernos.
En el tercer paso, se deshicieron los cambios anteriores y se variaron los ME a lo largo del rotor. El menor error fue el arrojado por este tercer paso.
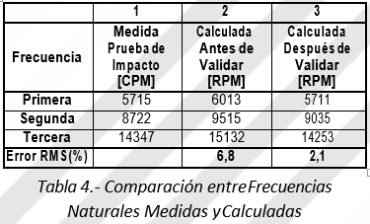
La comparación de las frecuencias críticas calculadas (del modelo) contra las medidas, antes y después de la calibración, se muestra en la Tabla 4. Antes de la calibración el error RMS fue 7%. Después de la calibración se obtuvo un 2%.
La Tabla 5 muestra un resumen del proceso de calibración y la configuración del rotor en lo que a módulos de elasticidad se refiere. Antes de calibrar el modelo, sólo se conocía la metalurgia de los pernos y discos de potencia, tal como se aprecia en la columna 2. Para validar el modelo en frío, se infirió que las zonas cuya metalurgia se desconocía eran de acero AISI 4140, con ME = 29,7 ksi (ver Tabla 5, columnas 4 y 5). No existen pernos en este modelo, por efecto de la reducción geométrica explicada anteriormente.
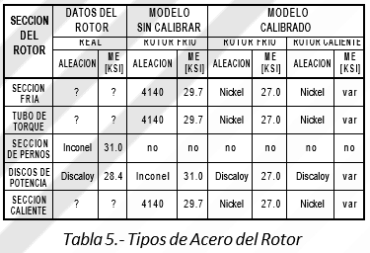
La calibración comenzó infiriendo que los discos de potencia se comportarían como si estuvieran construidos con el acero de los pernos (Inconel). Después de la calibración en frío, se concluyó que el rotor se comporta como si estuviera en su totalidad construido con un acero ligeramente mas elástico que un acero al nickel, mostrando un ME = 27 ksi (ver Tabla 5, columnas 6 y 7). Esto último, es consecuencia de la fricción interna entre los diferentes ensamblajes apernados y prensados. Sin embargo, se sabe que los discos de potencia son de acero Discaloy el cual exhibe, en este rotor, un ME reducido de también 27 ksi.
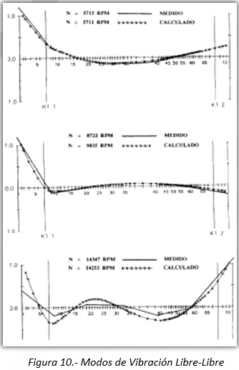
La Figura 10 muestra los modos de vibración libre-libre medidos en la prueba de impacto, superpuestos sobre los modos de vibración obtenidos con el programa de velocidades críticas CRTSP2 del laboratorio ROMAC de la Universidad de Virginia, EEUU.
Se observa en la Figura 10 que hay un acuerdo casi perfecto entre los modos calculados y los medidos, con la excepción del tercero. Sin embargo, en el tercer modo la discrepancia ocurre principalmente en las amplitudes (que no son determinantes), mientras los nodos coinciden de manera aceptable.
PROPIEDADES ELÁSTICAS DEL ROTOR EN CALIENTE
Gradiente Térmico a lo Largo del Rotor
El fabricante de la turbina fue consultado sobre este controversial hecho. Este suministró las temperaturas mostradas a continuación, las cuales sirvieron para establecer el gradiente de temperaturas de trabajo a lo largo del rotor:
Etapa 1 de potencia, acople cúrvico: 750 ºF Última etapa del compresor axial: 500 ºF Muñones: 150 ºF
Módulos de Elasticidad en Caliente
La validación dinámica es un proceso realizado a temperatura ambiente. Sin embargo, sirvió para determinar el módulo de elasticidad equivalente del rotor a temperatura ambiente.
Este módulo de elasticidad equivalente corresponde a un modelo de rotor constituido, en este caso, por dos tipos de acero: acero al nickel (ME = 27.8 ksi) reducido en 0.8 ksi, y acero Discaloy (ME = 28.4 ksi) reducido en 1.4 ksi.
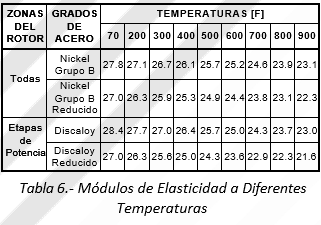
Para determinar los módulos de elasticidad a las temperaturas establecidas en 14.1, se construyó la Tabla 6. Se observa que, a temperatura ambiente, el Discaloy es mas rígido que la aleación al nickel. Sin embargo, a altas temperaturas el Discaloy es más elástico.
MODELO EN CALIENTE
La porción del modelo elastomásico en caliente correspondiente a las zonas adyacentes a la primera etapa de potencia (estaciones 41 á 48), se presenta en la Tabla 7. Las propiedades inerciales y elásticas están separadas por una línea horizontal. Se observa densidad cero (0), como corresponde al modelaje de eje sin masa desarrollado con el objetivo previo de variar independientemente las propiedades inerciales y elásticas durante el proceso de calibración.
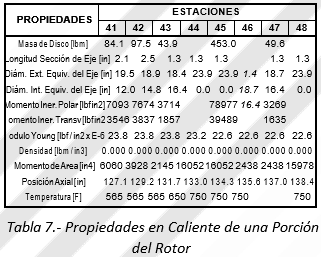
Las masas de los discos corresponden a la sección entera cuya longitud se muestra en la segunda fila. Igualmente los momentos de inercial transversales y polares. Los diámetros internos y externos son equivalentes, y corresponden al eje elástico sin masa. Se muestran otros parámetros de interés.
CONCLUSIONES
Generales
- El método de integración directa no es imprescindible para reducir secciones cónicas. El tratamiento geométrico manual empleado en este trabajo fue exitoso.
- Los diámetros axialmente equivalentes pueden ser calculados fácilmente utilizando la Ecuación 1, evitando así la construcción de la curva del momento flector.
- Las propiedades inerciales y elásticas de ensamblajes internamente apernados permanecen constantes a medida que el rotor gira.
- Los rotores ensamblados con pernos exhiben módulos de elasticidad reducidos, por efecto de la fricción entre sus partes.
- Como trabajo futuro, se propone el desarrollo de un método para validar modos de vibración.
Particulares
- El uso de los diámetros externos de las ruedas del compresor axial, como diámetros de rigidez, no tuvo éxito para validar el
- El rotor se comporta como si estuviera construido todo con acero al nickel y Discaloy, ambos de elasticidad
- Los modos de vibración medidos y calculados ajustan
- El 2% de error RMS obtenido por este modelaje permitirá hacer predicciones rotodinámicas
- Adicionalmente, este modelo simplificado permitirá estudiar el efecto que tengan en la dinámica del rotor, los cambios en la geometría y en las propiedades termomecánicas de los varios elementos que lo componen, como por ejemplo: cojinetes, acople, tubo de torque, diafragma, eje del compresor axial,
PASOS SIGUIENTES
Actualmente se realizan predicciones de respuesta forzada, utilizando el programa RESP2V3 del Laboratorio ROMAC. Estas predicciones se ajustan a las lecturas de campo con el mismo error (2%) obtenido durante la validación dinámica de este modelaje. Para esto se utiliza un modelo rotor-cojinete que fue desarrollado incorporando el efecto de los pedestales en forma de un sistema masa-resorte-amortiguador. También el acople fue analizado e incorporado en el modelo. Ambos, acople y pedestales, han mostrado tener un efecto marcado en la respuesta sincrónica del rotor.
Lagoven, S.A., en vista de la confiabilidad de las predicciones rotodinámicas realizadas con este modelo, planifica extender el alcance de este trabajo mas allá del balanceo en sitio inicialmente establecido. Entre los nuevos objetivos que se estudian están la retroadaptación de cojinetes y acople, y la revisión de las holguras en los sellos, a la luz de las amplitudes máximas predecibles a lo largo del rotor.
REFERENCIAS
- Infante, L.; Villavicencio, I; Reddy, V y Borjas, L. Modelo Elastomásico del Rotor del Compresor BCL356. Informe Intevep de Servicios Técnicos Especializados INT-TEIG-0060,95. Venezuela,
- Infante, L.; Azuaje, B.; Reddy, y Borjas,
- Modelo Elastomásico de Eje Denso del Rotor de la Turbina 1SU3. Informe Intevep de Servicios Técnicos Especializados INT-TEIG-0059,95. Venezuela, 1995.
- Childs, Turbomachinery Rotordynamics, Phenomena, Modeling and Analysis. John Wiley. New York, 1993.
- Vance, J. Rotordynamics of Turbomachinery. John Wiley. New York,
- Ehrich, Handbook of Rotordynamics. McGraw – Hill, Inc. USA, 1992.
- Tallavó, F y Martínez M. Pruebas de Impacto y Análisis Modal Experimental del Rotor W101. Informe Intevep de Servicios Técnicos Especializados INT-TEIG-0061,95. Venezuela,
- Taylor, D. y Barrett, L. The Use of Impact Testing to Measure the Modal Properties of Turbomachine Rotors. Romac Laboratories, University of Virginia. Report ROMAC 266. USA,